Picture this: you’re at a dinner party, and someone asks, “What’s a trapezoid?” Suddenly, all eyes are on you. Panic sets in as you realize you might not know the answer. But fear not! The trapezoid is more than just a quirky shape; it’s a geometric wonder that can make you the star of any conversation.
Table of Contents
ToggleDefinition of a Trapezoid Shape
A trapezoid is a four-sided polygon, known as a quadrilateral. It features at least one pair of parallel sides, which distinguishes it from other quadrilaterals. The parallel sides are referred to as the bases, while the non-parallel sides are called the legs. Trapezoids vary in shape; they can be right, isosceles, or scalene.
In a right trapezoid, one leg is perpendicular to the bases. An isosceles trapezoid has legs of equal length, creating symmetry. A scalene trapezoid possesses legs of different lengths, lacking this symmetry.
The area of a trapezoid can be calculated using the formula:
[
text{Area} = frac{(b_1 + b_2) times h}{2}
]
where ( b_1 ) and ( b_2 ) are the lengths of the bases and ( h ) is the height. This formula accounts for the varying lengths of the parallel sides, making it effective for a wide range of trapezoid shapes.
Understanding the definition of a trapezoid aids in recognizing its applications in real life. Trapezoids appear in architecture, design, and various engineering fields. They also provide a basis for exploring more complex geometric concepts.
Recognizing trapezoids enhances mathematical comprehension. Familiarity with the trapezoid leads to improved problem-solving skills, facilitating engaging discussions on geometry.
Characteristics of a Trapezoid Shape
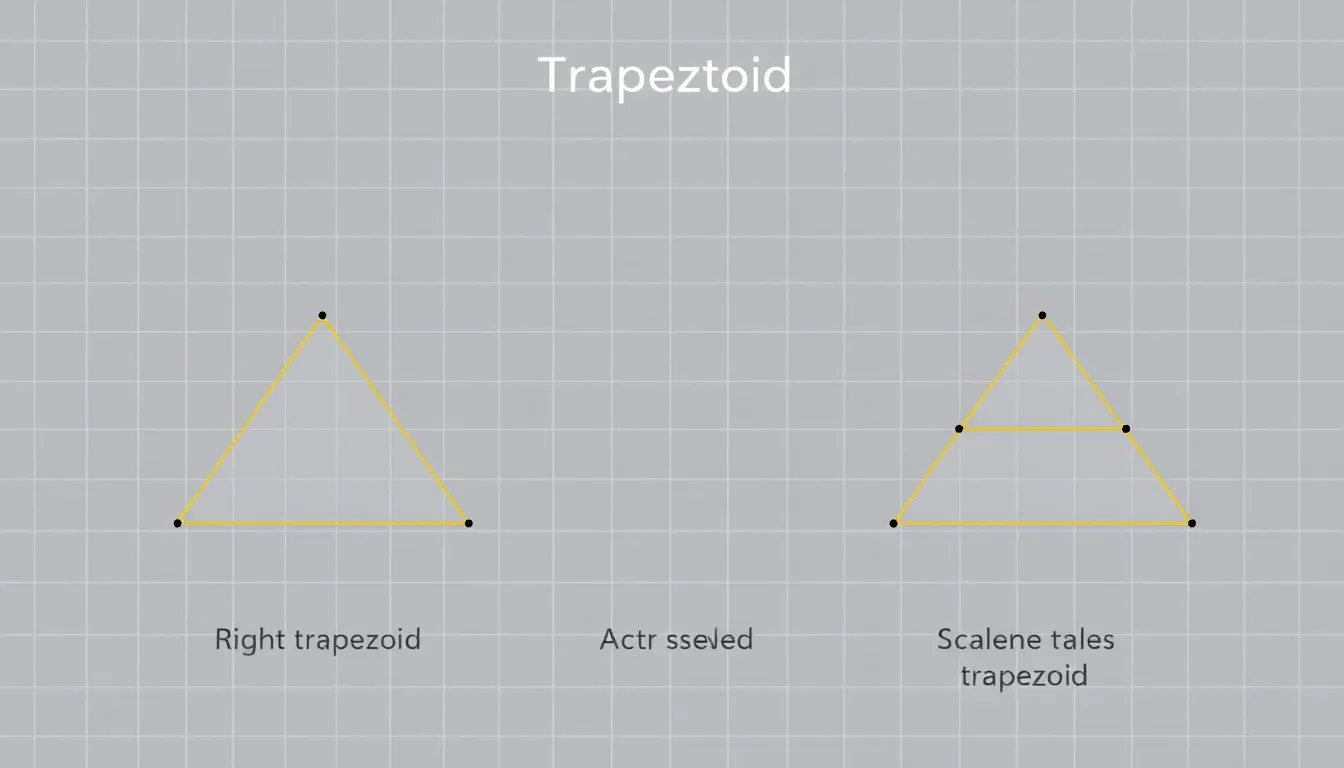
Trapezoids exhibit unique features that distinguish them from other shapes. They consist of four sides, with at least one pair of parallel sides called the bases.
Types of Trapezoids
Different types of trapezoids include right trapezoids, isosceles trapezoids, and scalene trapezoids. Right trapezoids have one leg perpendicular to their bases, creating a distinct right angle. Isosceles trapezoids possess legs of equal length, resulting in symmetrical properties. Scalene trapezoids, in contrast, feature legs of differing lengths, leading to a more irregular appearance. Each type serves different purposes in geometry and applied fields.
Properties and Measurements
Several properties define trapezoids mathematically. The area can be calculated with the formula: Area = (Base1 + Base2) x Height / 2. This formula incorporates the lengths of the bases and the height between them. Additionally, trapezoids have a sum of interior angles equal to 360 degrees. The lengths of the legs contribute to understanding trapezoid dimensions. Knowing these properties allows for practical applications in various fields, reinforcing the importance of trapezoids in geometry.
Real-World Examples of Trapezoid Shapes
Trapezoids appear in various real-world applications, showcasing their unique geometric properties. Buildings commonly use trapezoidal shapes in architecture for aesthetic appeal and structural stability. A great example includes rooftop designs, where sloped sides create efficient drainage systems.
Bridges often incorporate trapezoidal beams, taking advantage of their strength and ability to distribute weight evenly. The design minimizes material use while maintaining integrity, proving beneficial in construction.
Additionally, road signs often adopt trapezoidal shapes for visibility. The wider top allows for more information display, while the tapered bottom aids in drawing attention from drivers.
Furniture designs frequently feature trapezoids as well, particularly in tables and bookcases. These shapes allow for creative use of space, enhancing both function and style.
Graphic design might utilize trapezoidal shapes in logos and marketing materials. The appealing angles can attract viewers, contributing to a brand’s identity.
Landscaping often embraces trapezoidal plots for gardens and patios. Such layouts maximize space efficiency and visual interest in outdoor design.
Overall, trapezoids are integral to many everyday objects and structures. Their versatility allows for innovative uses across diverse industries, highlighting the significant role of this geometric shape in our lives.
Importance of Trapezoid Shapes in Geometry
Trapezoids play a significant role in geometry, highlighting the diversity of quadrilaterals. Their unique property of having at least one pair of parallel sides allows for various applications in mathematical problems. Understanding trapezoid types enhances comprehension of geometric relationships; for example, right trapezoids promote the study of angles and perpendicular lines.
Applications in architecture showcase the importance of trapezoids. Rooftops often incorporate trapezoidal designs to ensure efficient water drainage, decreasing the likelihood of structural damage. Bridges utilize trapezoidal beams to provide strength and assist in weight distribution, making these shapes essential for safety and durability.
In educational settings, trapezoids aid in teaching fundamental concepts. Students grasp ideas related to area calculation using the formula Area = (Base1 + Base2) x Height / 2, reinforcing their understanding of area across different shapes. Additionally, the sum of the interior angles, totaling 360 degrees in a trapezoid, supports the learning of angle properties.
Real-world examples enhance the appreciation of trapezoidal shapes. Road signs often adopt trapezoidal shapes for improved visibility, capturing the attention of drivers. Furniture designs frequently incorporate trapezoids to optimize space usage, merging aesthetics with functionality. Graphic designers utilize trapezoidal forms in logos, creating memorable visuals that stand out.
Overall, trapezoids serve as a bridge between theoretical concepts and practical applications. Mastering the properties of trapezoids leads to improved problem-solving capabilities and fosters engaging discussions in geometry. Their versatility ensures relevance across various fields, making them indispensable in both academic and real-world contexts.
Understanding trapezoids enriches one’s knowledge of geometry and its practical applications. Their unique properties and versatile forms make them essential in various fields from architecture to graphic design. Mastering the concepts associated with trapezoids not only boosts mathematical skills but also enhances everyday discussions about shapes and structures. Embracing these geometric figures opens up new avenues for creativity and problem-solving, proving that even a simple trapezoid can have a significant impact on both academic and real-world scenarios.



